Attention and Transformer
目录
本文记录自己初学Transformer的笔记,内容大部分参考这篇Blog
Overview
将Prompt输入到大模型后,大模型以Token为单位一个个输出,如下图所示:

每一个输出的Token,都会被添加到Prompt中指导下一个输出,这样的模型也被称为Autoregressive models。与之相反,Bert不是自回归模型。

在这个过程中,Transformer是其中的关键组件,而transformer的技术要点则是self-attention机制。
Self-Attention
Attention计算的总结:

单个input的计算
假设进行一个翻译任务,以下是翻译的句子:
The animal didn't cross the street because it was too tired
it究竟指代什么?Self-Attention帮助神经网络理解这个问题,它将通过一系列计算建立it和其余token的关联程度。
首先,有$W^Q,W^K,W^V$ 矩阵,去得到query、key、value,对于一个input的计算过程如下:
- input被tokenizer和embedding的方法转化为embedding $x_1$,假设其维度为512维。
- $W^Qx_1,W^Kx_1,W^Vx_1$得到$x_1$对应的$q_1、k_1、v_1$。$q_1$和$k_1$的维度应该相同,因为要用它们的内积代表注意力分数,$v_1$的维度可以按需要而定。
- $q_1\cdot k_1 $得到注意力分数,假设为112。
- 然后,注意力分数除以$\sqrt d_k$,这样就得到了第一个input和自己的注意力分数。效仿这个做法,将$q_1\cdot k_2$得出第一个input和第二个input之间的注意力分数。
- 当得出了第一个input和所有input之间的注意力分数,例如下图中,得到了$\alpha_1,\alpha_2$,用它们将values线性组合得出第一个input经过一层self-attention的输出$z_1=\alpha_1v_1+\alpha_2v_2$,直观上,这种组合结合了input序列的所有信息,并且利用attention分数对信息的重要程度进行了加权。

矩阵计算
使用矩阵计算增加了计算的并行度,提高了计算效率。
所有input组成矩阵$X$, 和$W^Q、W^K、W^V$矩阵相乘,得到$Q、K、V$。

然后,按照以下公式得出这一层的输出$Z$,下图中,Z的每一行都是对应input的输出。

Muti-heads Attention
每个 Attention head都有自己的$W^Q,W^K,W^V$,每个注意力头都会产生一个$Z$作为输出,将每个注意力头产生的$Z$按照一定方法结合起来,比如相加、连接等。

多头的好处在于能增加表示空间,不同的$W^Q,W^K,W^V$能分别表示不同的语义信息,关注不同的状态。
Transformer
Enocder
位置编码
以上所提到的Self-Attention机制不包含位置编码,对于这样的Attention而言token的输入顺序是无关紧要的,cat bites mouse和mouse bites cat对以上的Attention并无区别,例如最后的输出是矩阵$Z$,cat bites mouse和mouse bites cat这两个输入序列的不同仅仅在于cat和mouse对应的输出行互换了,模型看来都是一样的结果。
但是对于各种text-generation、分类的任务而言,位置信息是很有必要的,所以Transformer的encoder要通过嵌入位置向量表示信息。位置信息的嵌入有很多方法,此处不赘述。

残差连接
Encoder中的Add&Normalize是一个残差块,将$Z$和$X$相加,然后归一化,现在,有些模型把layerNorm放在self-Attention之前。

Decoder
Decoder的架构和Encoder非常相似,不同之处在于Encoder-Decoder Attention(Cross-Attention),这是为了Encoder和 Decoder的交互设计的。

而且,Decoder中的Self-Attention加入了mask,只会看见输出之前的token。Encoder最终的输出被作为K、V在 Encoder-Decoder Attention中起作用。Decoder产生的输出将继续作为整个Decoder的输入。
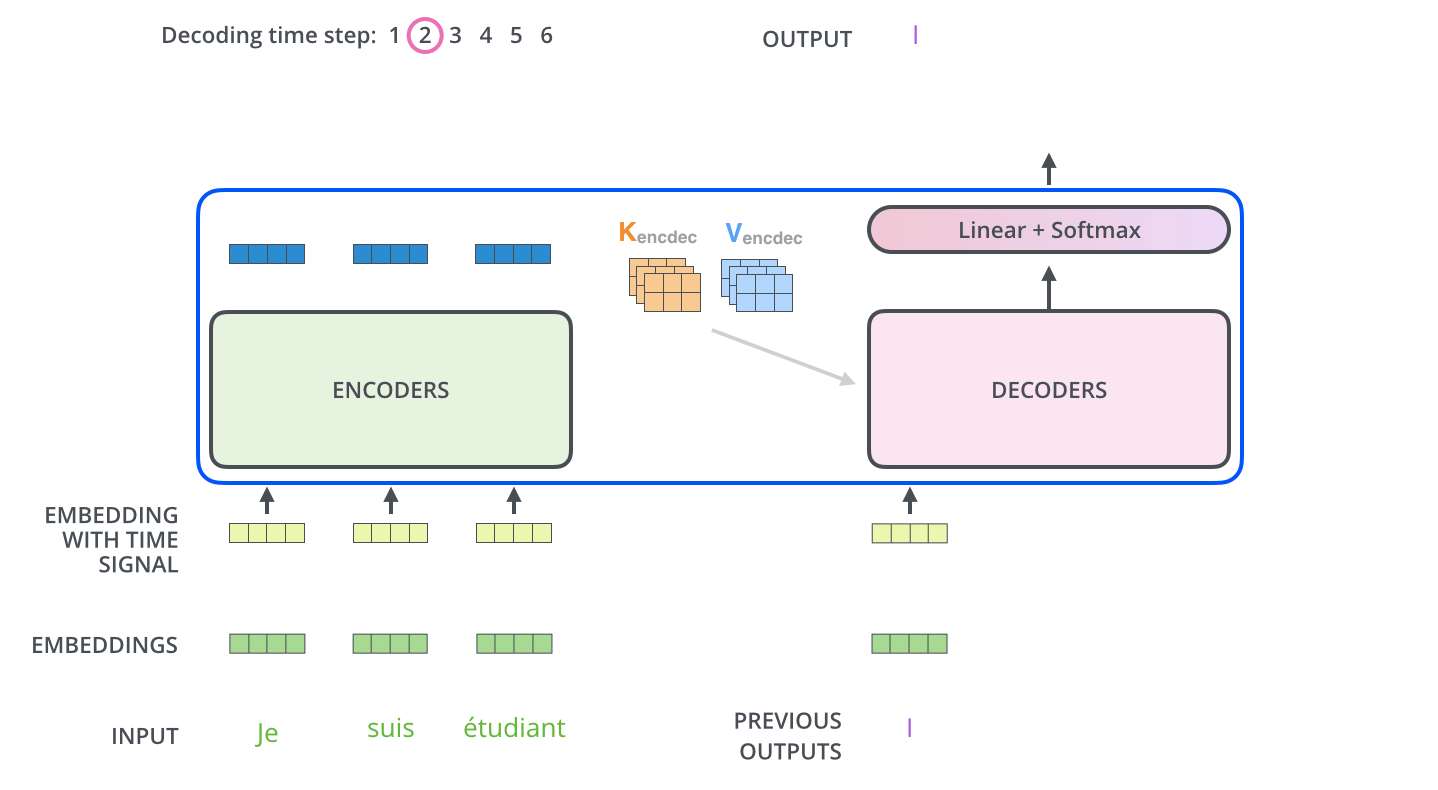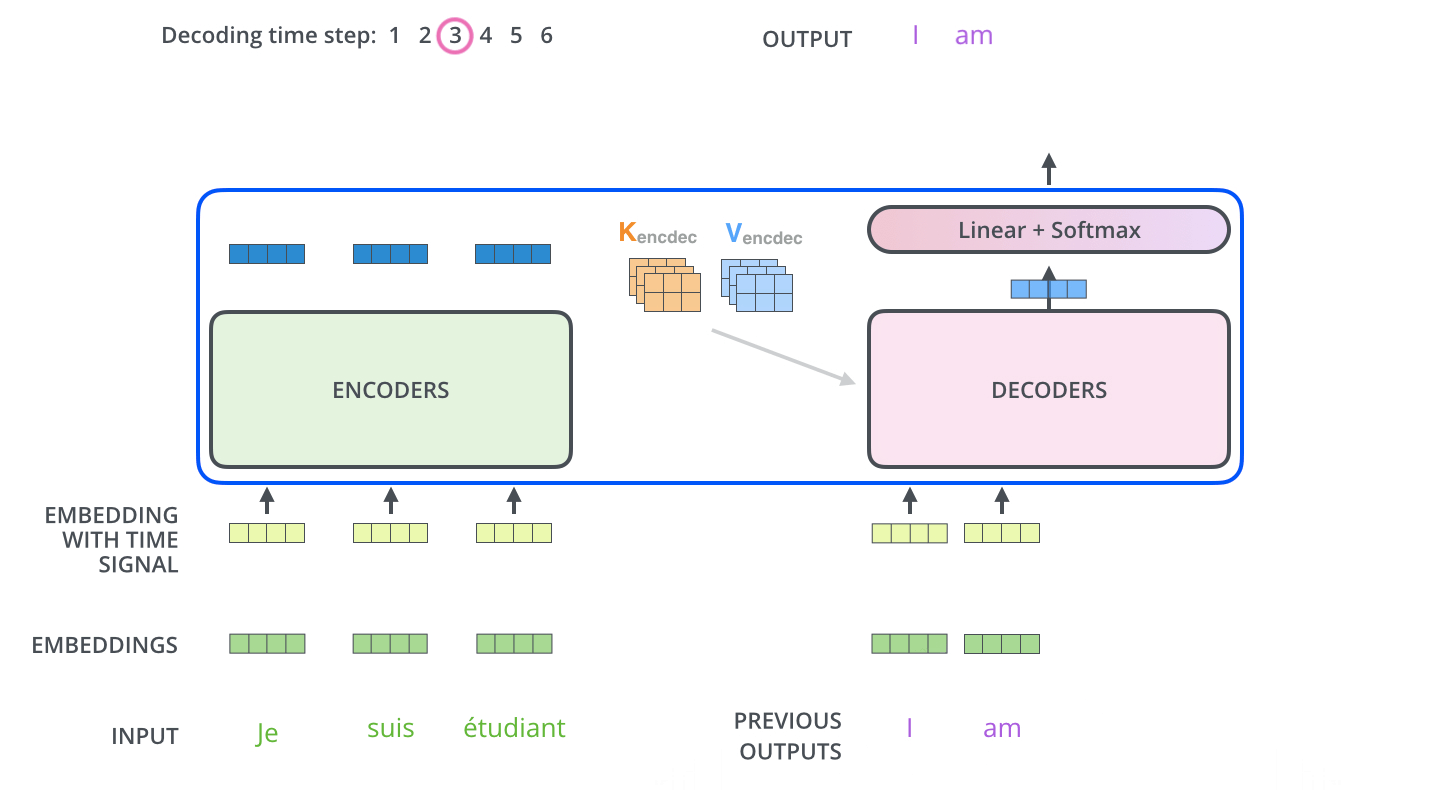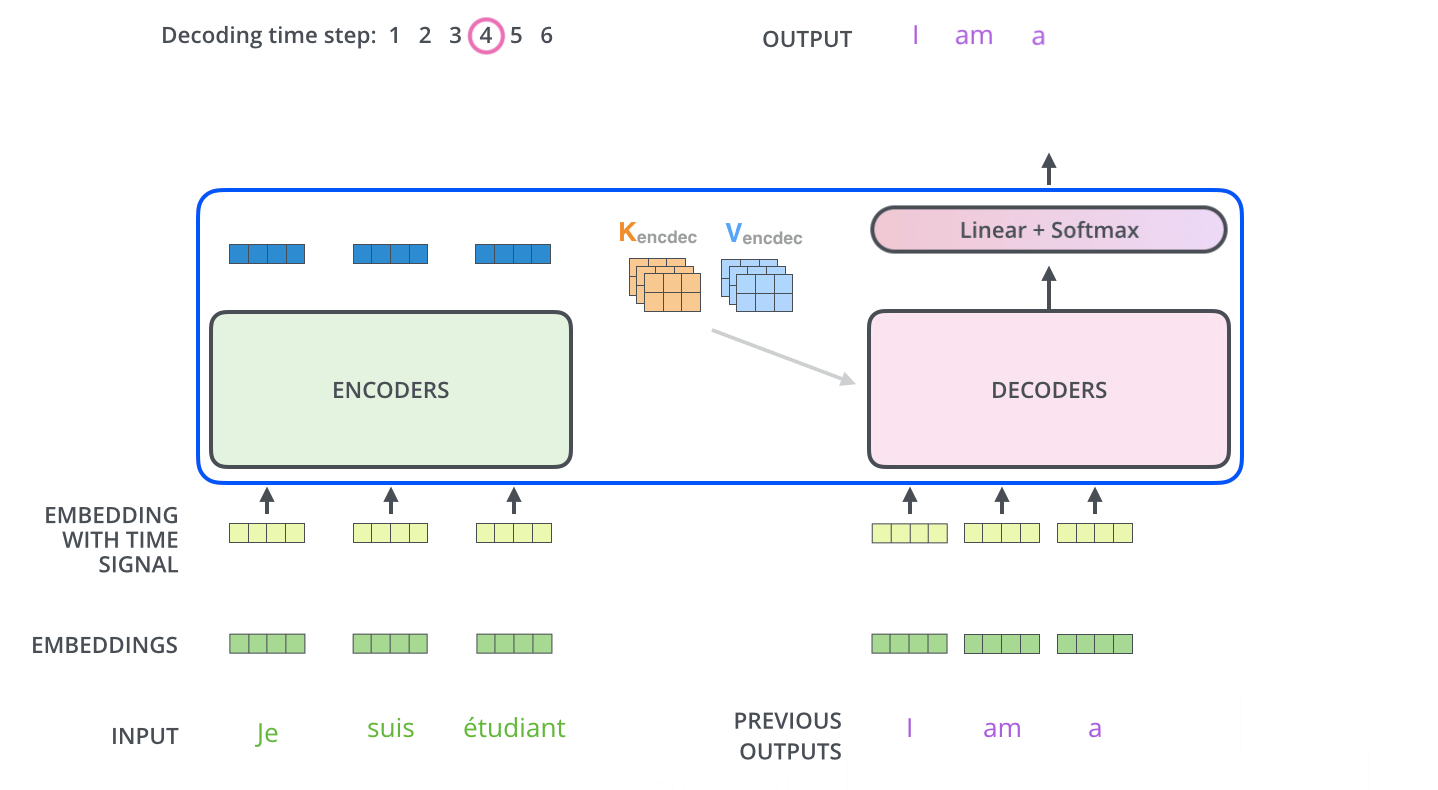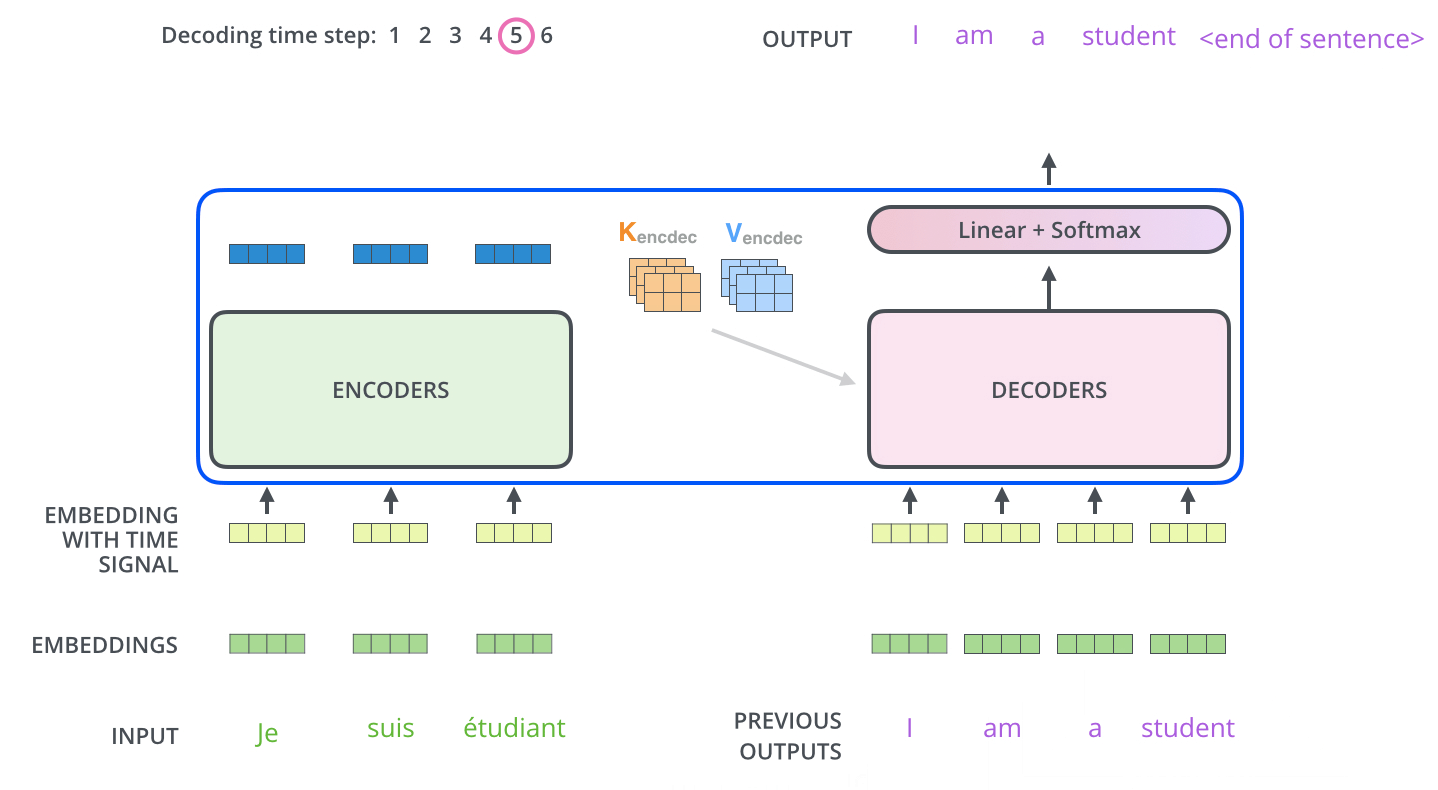
这样的解码过程由输入Begin token开始,直到 END结束。

分享这篇文章